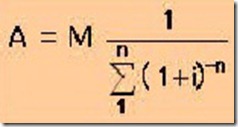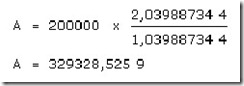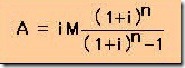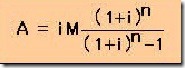Kompetensi Dasar
Menerapkan metode kuantitatif
Indikator
1. Mengidentifikasi karakteristisk anuitas
2. Menghitung anuitas
Materi
Pengertian Anuitas
Anuitas adalah suatu pembayaran yang jumlahnya sama, yang diterima atau dibayarkan pada tiap akhir periode dengan waktu yang sama untuk jumlah waktu tertentu. Sedangkan angsuran adalah suatu pembayaran dengan jumlah tertentu, yang mungkin jumlahnya dapat berbeda dan waktu dapat tidak teratur. Tetapi pada anuitas jumlah pembayaran sama dan jangka waktu juga sama.
Karakteristik Anuitas
Anuitas memiliki karakteristik sebagai berikut :
- Jumlah yang dibayarkan tiap periodenya sama.
- Jangka waktunya sama.
- Suku bunga yang diberlakukan tertentu.
Contohnya pada kredit yang diberikan pihak bank, kredit perumahan, kredit kendaraan bermotor atau kredit barang elektronik.
Menghitung Anuitas
Besar Anuitas
Besar anuitas adalah besarnya angsuran ditambah dengan bunga yang diperhitungkan.
| Anuitas = Angsuran + Bunga |
Misal :
Pak Thomas tiap bulan membayar kredit rumahnya yang terdiri dari angsuran sebesar
Rp. 300.000,00 dan bunga sebesar Rp. 125.000,00,
maka:
anuitas yang dibayarkan adalah Rp. 425.000,00 (Rp.300.000,00 + Rp. 125.000,00).
Artinya:
anuitas kredit rumah yang harus dibayar Pak Thomas tiap bulan sebesar Rp. 425.000,00.
Menghitung Besarnya Anuitas
Untuk menentukan besarnya anuitas digunakan pula rumus sebagai berikut :
Agar lebih jelas menggunakan rumus tersebut perhatikan contoh berikut !
Josima meminjam uang dari Bank BRI sebesar Rp. 10.000.000,00 pembayaran dilakukan dengan cara anuitas dengan memperhitungkan bunga 2% per bulan. Pinjaman lunas selama 3 tahun dengan pembayaran bulanan. Berapa jumlah pembayaran (anuitas) yang harus dibayar Josima tiap bulan?
Penyelesaian :
Diketahui : M = Rp. 10.000.000,00
i = 2% per bulan
n = 3 tahun = 36 bulan
Rumus :
Maka :
Jadi, besarnya Anuitas adalah sebesar Rp. 329.328,53
Anuitas dan Pembulatan
Bila diperhatikan perhitungan anutas sebelumnya nilai rupiah kurang realistis, karena hasilnya lebih dari dua angka dibelakang koma, sedangkan kenyataannya pembayaran dalam pecahan rupiah pun sulit dilakukan. Oleh karena itu agar hasilnya lebih realistis dilakukan pembulatan.
Pembulatan dapat dilakukan dalam puluhan rupiah, ratusan rupiah atau ribuan rupiah baik keatas maupun kebawah.
Misal nilai anuitas sebesar Rp. 16,461,721.82 dibulatkan sebagai berikut :
Dalam puluhan rupiah menjadi Rp. 16.461.720,00
Dalam ratusan rupiah menjadi Rp. 16.461.700,00
Dalam ribuan rupiah menjadi Rp. 16.462.000,00
Akibat pembulatan tersebut akan terjadi kelebihan atau kekurangan pembayaran. Kelebihan atau kekurangan ini diperhitungkan pada pembayaran anuitas terakhir.
Jadi besarnya Anuitas adalah sebesar Rp. 329.328,53
Agar lebih jelasnya, ikutilah contoh ini:
Andra meminjam uang sebesar Rp. 50.000.000,00 pinjaman itu akan dilunasi dengan cara anuitas selama 2 tahun yang pembayarannya setiap 6 bulan. Bunga yang ditetapkan 24% per tahun. Hitunglah besarnya Anuitas yang dibulatkan dalam ratusan rupiah dan buatlah tabel rencana angsuran !
Penyelesaian :
Diketahui : M = Rp. 50.000.000,00
i = 24% per tahun = 12% per 6 bulan (semester)
n = 2 tahun = 4 semester
Rumus :
Maka:
Dibulatkan menjadi Rp. 16.461.700,00
Membuat Rencana Angsuran
Untuk memastikan benar tidaknya perhitungan sebaiknya disusun rencana pelunasan angsuran anuitas sampai terakhir. Pada anuitas terakhir angsuran utang jumlahnya harus nol. Jika ternyata tidak nol berarti ada kesalahan atau selisih terjadi karena pembulatan.
Agar lebih jelasnya, ikuti contoh berikut:
Andra meminjam uang sebesar Rp. 50.000.000,00 pinjaman itu akan dilunasi dengan cara anuitas selama 2 tahun yang pembayarannya setiap 6 bulan. Bunga yang ditetapkan 24% per tahun. Hitunglah besarnya Anuitas dan buatlah tabel rencana angsuran !
Penyelesaian :
Diketahui :
M = Rp. 50.000.000,00
i = 24% per tahun = 12% per 6 bulan (semester)
n = 2 tahun = 4 semester
Rumus :
A = 16.461.761,82
Menentukan Angsuran Periode Tertentu
Adakalanya kita ingin mengetahui, berapa angsuran pada periode tertentu. Besarnya angsuran pada periode tertentu dapat dihitung dengan rumus :
Atau menggunakan table rencana angsuran.
Keterangan :
an = Angsuran periode tertentu atau ke n
A = Anuitas
M = Jumlah uang yang dipinjam
i = Suku bunga
n = Periode tertentu atau ke n
Untuk jelasnya perhatikan contoh berikut!
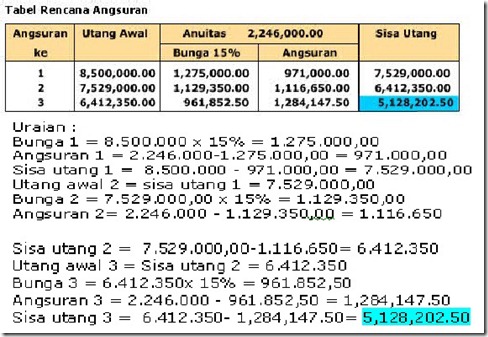
Dini memperoleh kredit sebesar Rp. 8.500.000,00 yang dibayar secara anuitas selama 6 tahun dengan anuitas sebesar Rp. 2.246.000,00 maka besarnya angsuran ke 3 adalah….
Penyelesaian :
Diketahui :
A = Rp. 2.246.000,00
M = Rp. 8.500.000,00
i = 15% per tahun
n = 3
Maka :
a3 = {2.256.000 – (8.500.000 x 0,15)}(1 + 0,15)3-1
= (2.256.000 – 1.275.000) x (1 + 0,15)3-1
= 971.000 x 1,152
= 971.000 x 1.3225
= 1.284.147,50
Dengan table:
Menentukan Sisa Utang Periode Tertentu
Adakalanya kita ingin mengetahui, berapa Sisa Utang pada periode tertentu. Besarnya sisa utang pada periode tertentu dapat dihitung dengan rumus :
Keterangan :
a1 = Angsuran periode ke 1 = A - Mi
A = Anuitas
M = Jumlah uang yang dipinjam
i = Suku bunga
n = Periode tertentu atau ke n
Untuk jelasnya perhatikan contoh berikut!
Dini memperoleh kredit sebesar Rp. 8.500.000,00 yang dibayar secara anuitas selama 6 tahun dengan anuitas sebesar Rp. 2.246.000,00 maka besarnya sisa utang ke 3 adalah...
Penyelesaian :
Diketahui :
A = Rp. 2.246.000,00
M = Rp. 8.500.000,00
i = 15% per tahun
n = 3
Maka :
a1 = A – Mi
SU3
= 2.246.000 – (8.500.000x0,15) =971.000
= 8.500.000 – 971.000{1 + ∑(1 + 0,15)3-1 }
= 8.500.000 – 971.000 {1 +∑(1,015)2 }
= 8.500.000 – 971.000 { 1 + 2.4725}
= 8.500.000 – 971.000 (3,4725)
= 8.500.000 – 3.371.797,50
= 5.128.202,50
Dengan tabel :
Menentukan Bunga pada Periode tertentu
Adakalanya kita ingin mengetahui, berapa Bunga pada periode tertentu. Besarnya bunga pada periode tertentu dapat dihitung dengan rumus :
Keterangan :
a1 = Angsuran periode ke 1 = A - Mi
A = Anuitas
M = Jumlah uang yang dipinjam
i = Suku bunga
n = Periode tertentu atau ke n
Untuk jelasnya perhatikan contoh berikut!
Dini memperoleh kredit sebesar Rp. 8.500.000,00 yang dibayar secara anuitas selama 6 tahun dengan anuitas sebesar Rp. 2.246.000,00 maka besarnya bunga pada periode ke 3 adalah….
Penyelesaian :
Diketahui :
A = Rp. 2.246.000,00
M = Rp. 8.500.000,00
i = 15% per tahun
n = 3
Maka :
a1 = A – Mi
Bunga 3
= 2.246.000 – (8.500.000x0,15) = 971.000
= 2.246.000 - 971.000 ( 1 + 0,15) 3-1
= 2.246.000– 971.000x 1,152
= 2.246.000– 971.000x1.3225
= 2.246.000– 1.284.147,50
= 961.852,50
Dengan tabel:
SimulasiLatihan